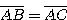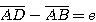|
Author: |
Zvonimir Durcevic |
|
Address: |
Kaiser-Ebersdorfer Straße 28-38/12/3, 1110 Vienna, Austria |
|
EMail: |
|
|
Date: |
08.01.2004 |
CONIC SECTIONS AND THEIR SPECIAL CASES
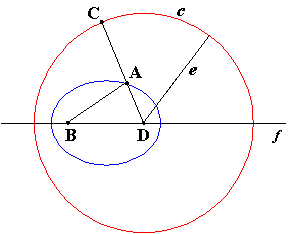
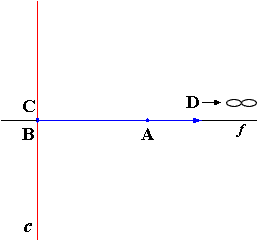
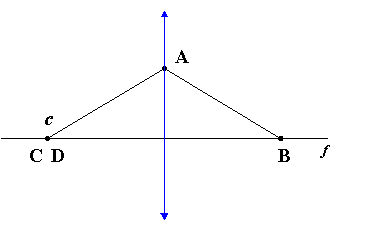
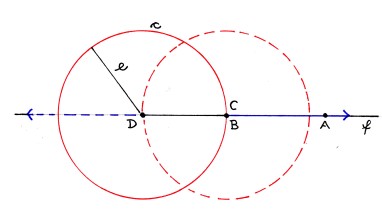
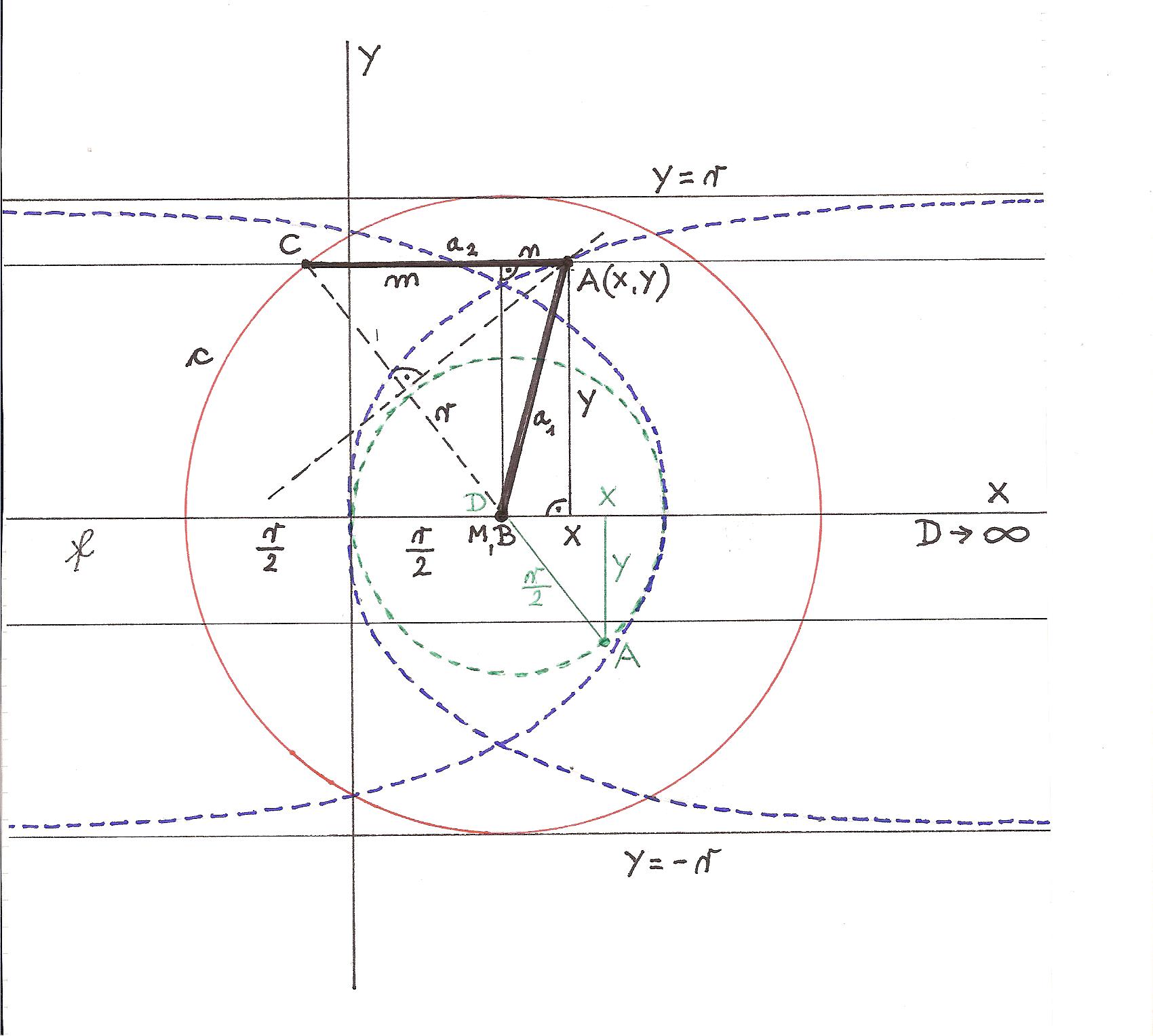
Construction of all conic sections (including parabola) by means of a fixed circle and a fixed point.Description in alphabetical order:
| A | - | The arbitrary point of all conic sections |
| B | - | The fixed point; the first focus |
| c | - | The fixed circle |
| C | - | The point on c |
| D | - | The center of c; the second focus |
| e | - | The radius of c |
| f | - | The axis |
According to this known construction the point A is the point of intersection between the straight line through C, D and the perpendicular bisector of the line segment BC. (AB = AC)
A is equidistant from B and c.
These drawings are the proof for the common construction of all conic sections by means of a fixed circle and a fixed point.
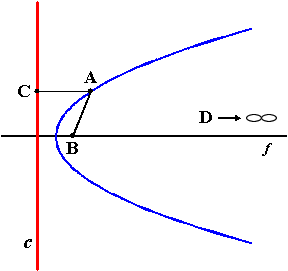
(Parabola: the center of the fixed circle is at infinity.)
|
The ellipse:
|
|
|
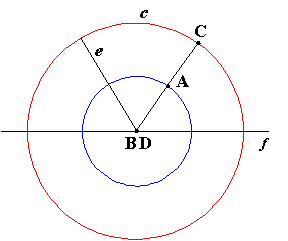
The circle:
The circle is a special case of the ellipse. |
|
|
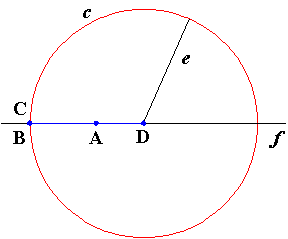
The line segment:
The line segment is a special case of the ellipse. |
|
|
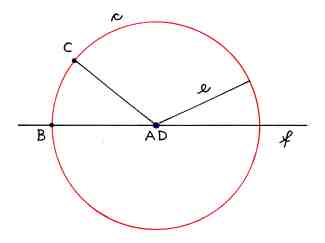
The parabola:
The infinite half ellipse.
|
|
|
The half line:
The half line is a special case of the parabola. |
|
|
The hyperbola:
The branch of the hyperbola.
|
 |
|
The straight line:
The straight line
is a special case of the hyperbola |
|
I would like to thank prof. Dr. Dörte Haftendorn (University Lüneburg, Germany) (www.doerte-haftendorn.de) for reviewing my work and putting an effort in creating WebPages (http://haftendorn.uni-lueneburg.de/mathe-lehramt/kurven/kegel/leitkreis/leitkreis.htm) with additional drawings and explanations.
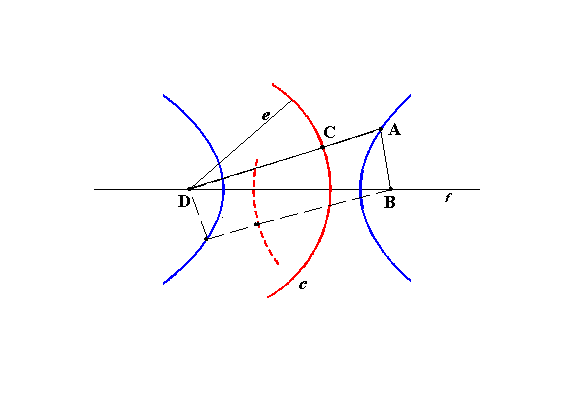
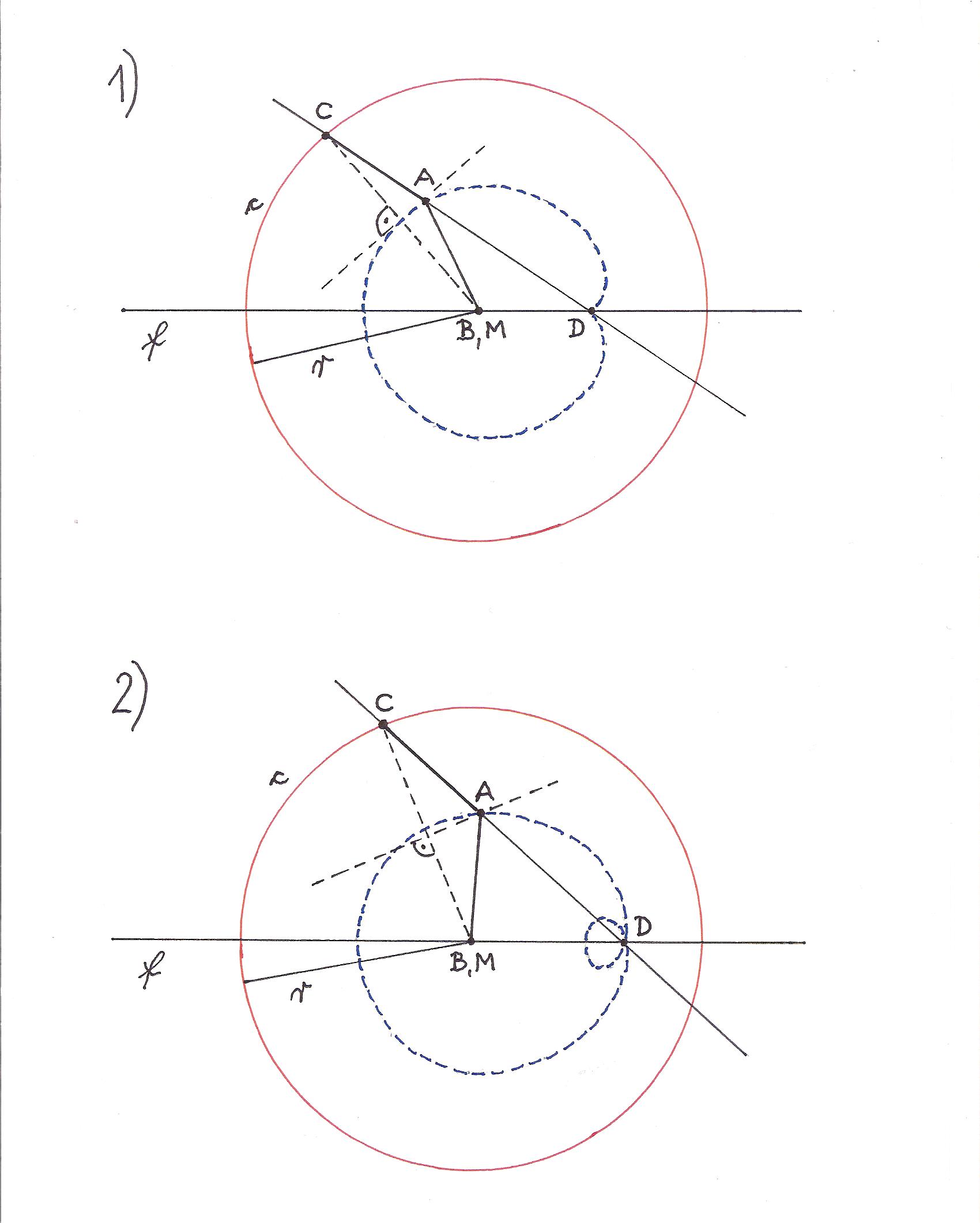
DISTORTED CONIC SECTIONS (GENERALIZED CONIC SECTIONS)
From the construction by a circle and a point.
(Construction by perpendicular bisector.)
The point of intersection of the straight lines is located outside the center of the circle.
Another interpretation of the construction by means of a fixed circle and a fixed point.
Additional interpretation of the points D, C:
D is the point of intersection between the secants of c.
C is the point of intersection between c and a secant.
A is the point of intersection between the secant and the perpendicular bisector of the line segment BC.
AB = AC
The line segment AC on the secant and the line segment AB have the same lengths.
B, D and the center of c can lie anywhere on the same secant.
(The f axis; symmetry axis)
If D is located in the center of c (the special case), the curves are the conic sections.
Because the secants are perpendicular to c, the both definitions apply:
- A is equidistant ...
- The line segment AC ...
If D is not located in the center of c, the curves are more or less distorted circles, ellipses, parabolas and hyperbolas. (Distorted conic sections)
B and D are no foci.
The closer D to the center of c, the less the curve is distorted.
The shape of a curve is determined by the positional relationship between B, D, c and the center of c.
There are a lot of shapes of these curves.
One example:
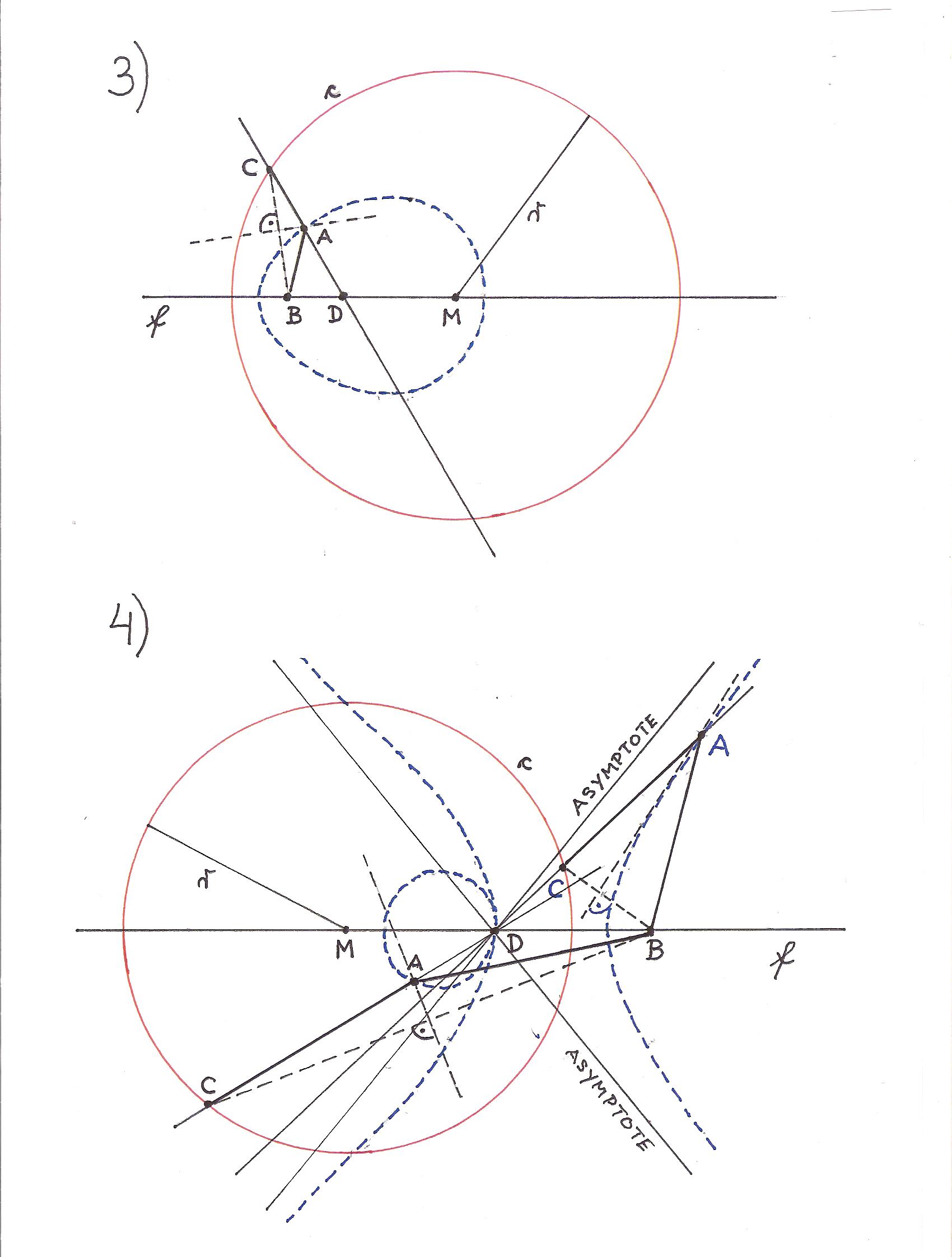
DISTORTED PARABOLA
(M - the center of c)
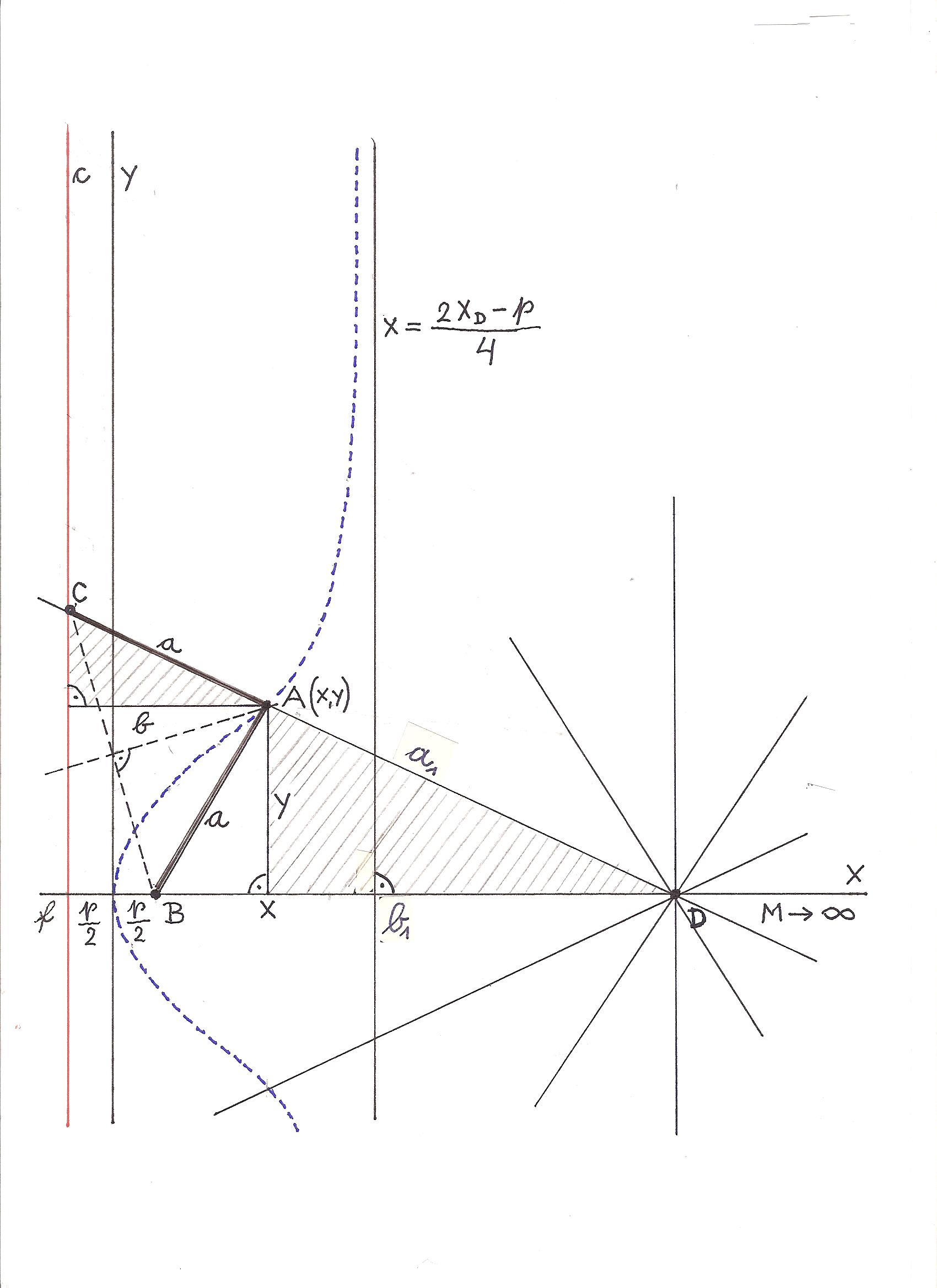
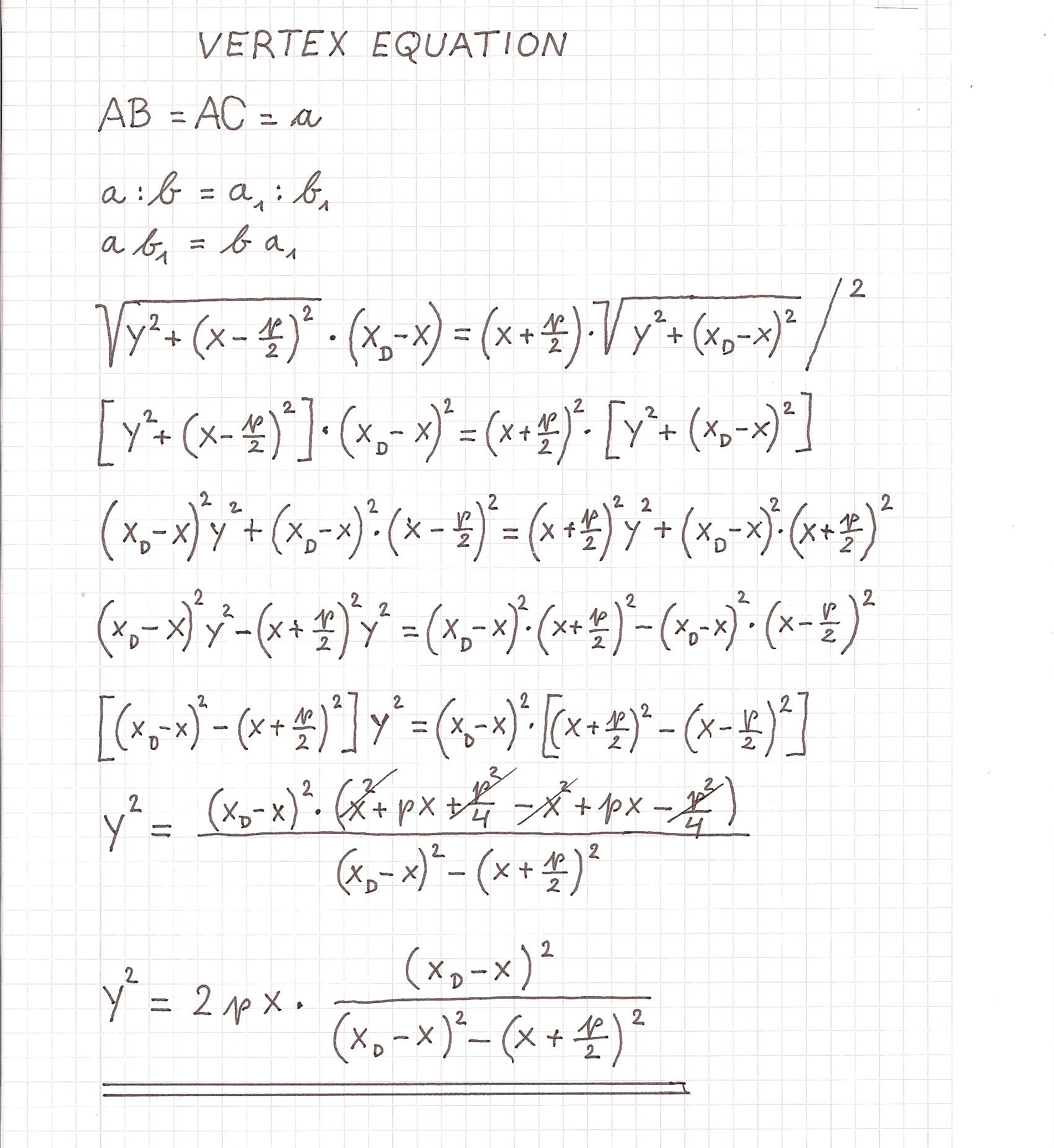
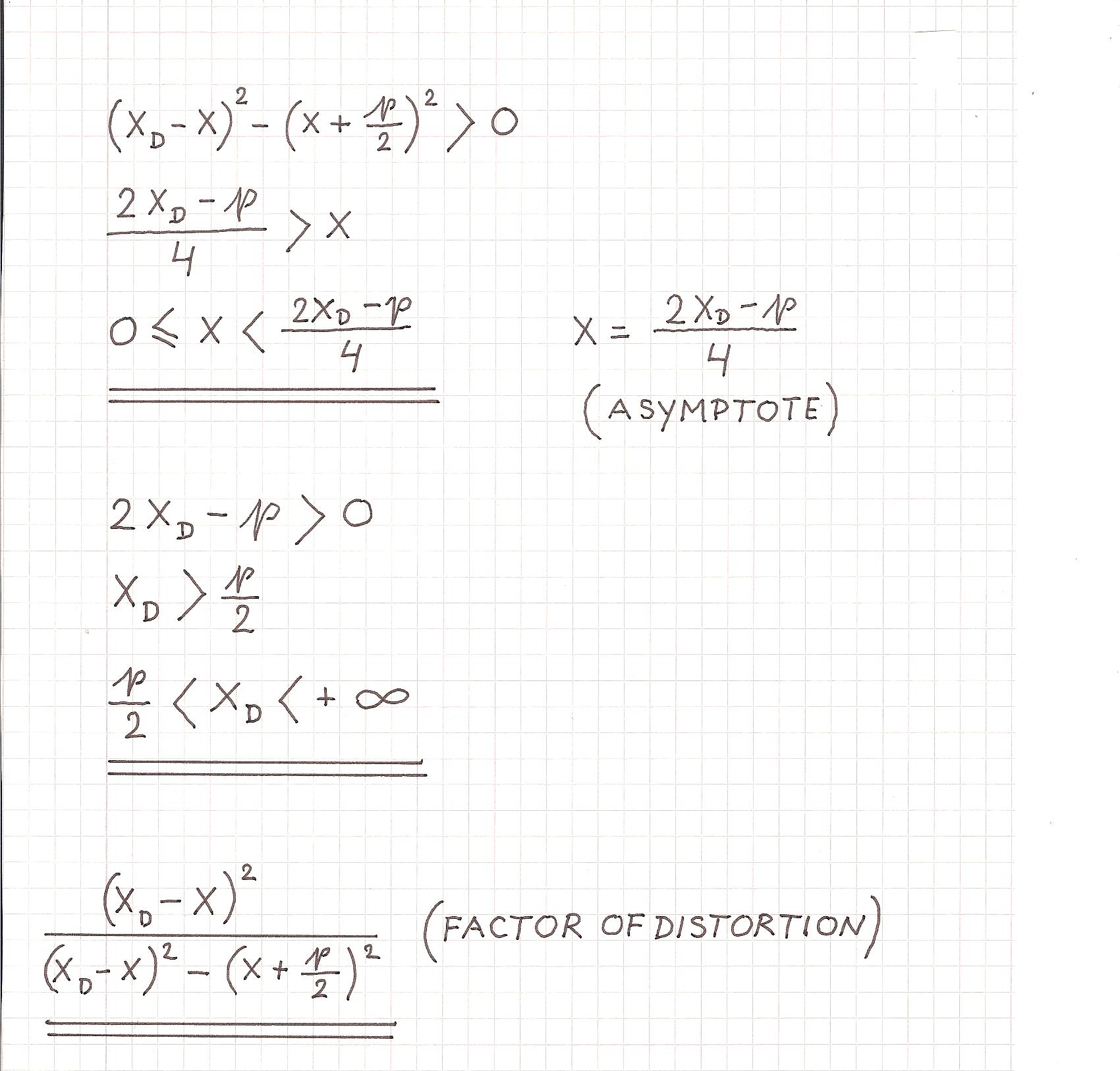
Distorted parabolas are given by p, xD.
The farther D is removed from B, the less the parabola is distorted.
If D is infinitely far from B, there is no distortion.
(xD -> ∞; Factor of distortion = 1; y2 = 2px)
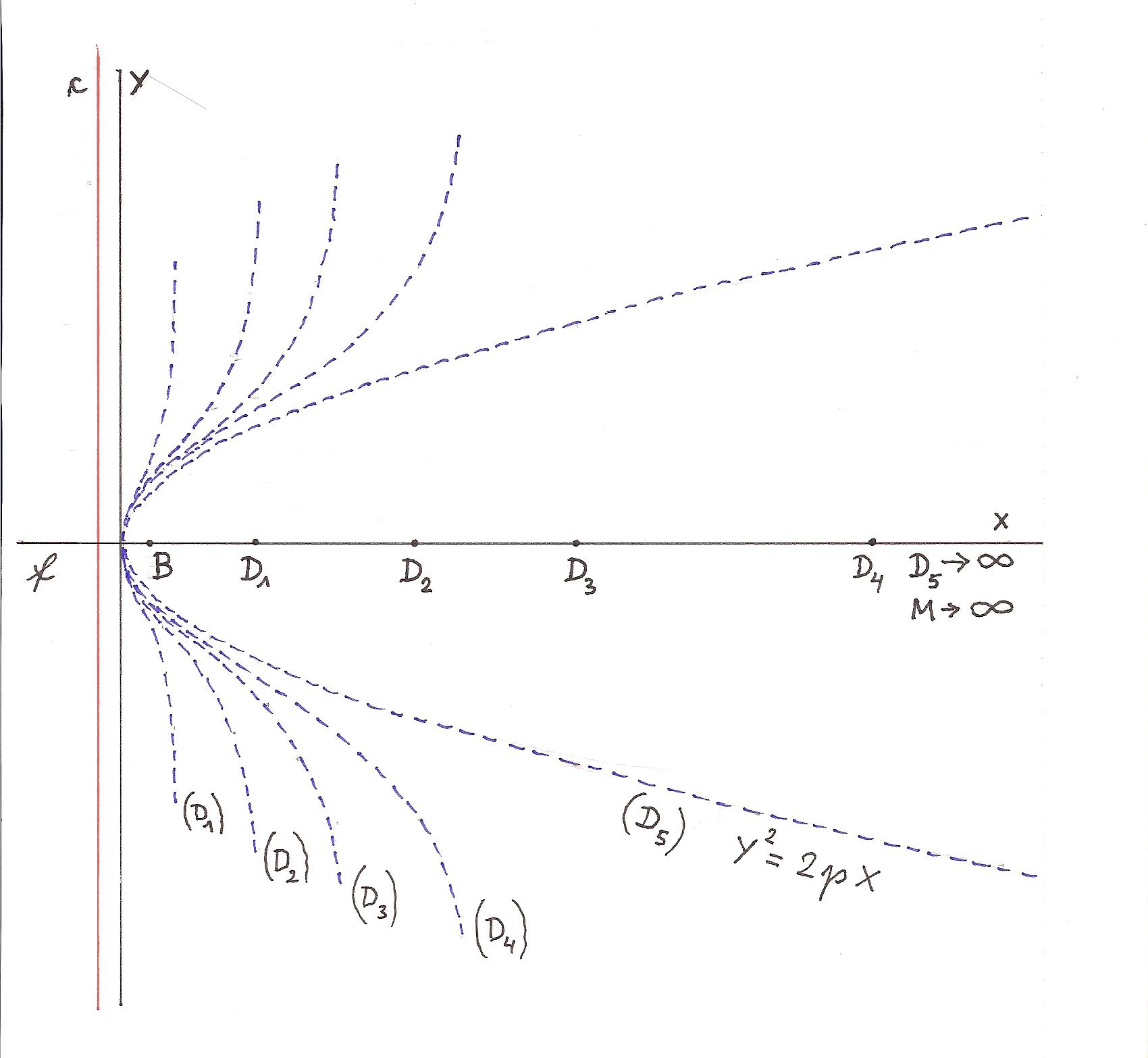
Another example:
DISTORTED CIRCLE
(B is located in the center of c.)
(M - the center of c; r instead of e)
D -> ∞; The secants are parallel to each other.
Some computer images of these curves created by Prof. Dr. Georg Glaeser.
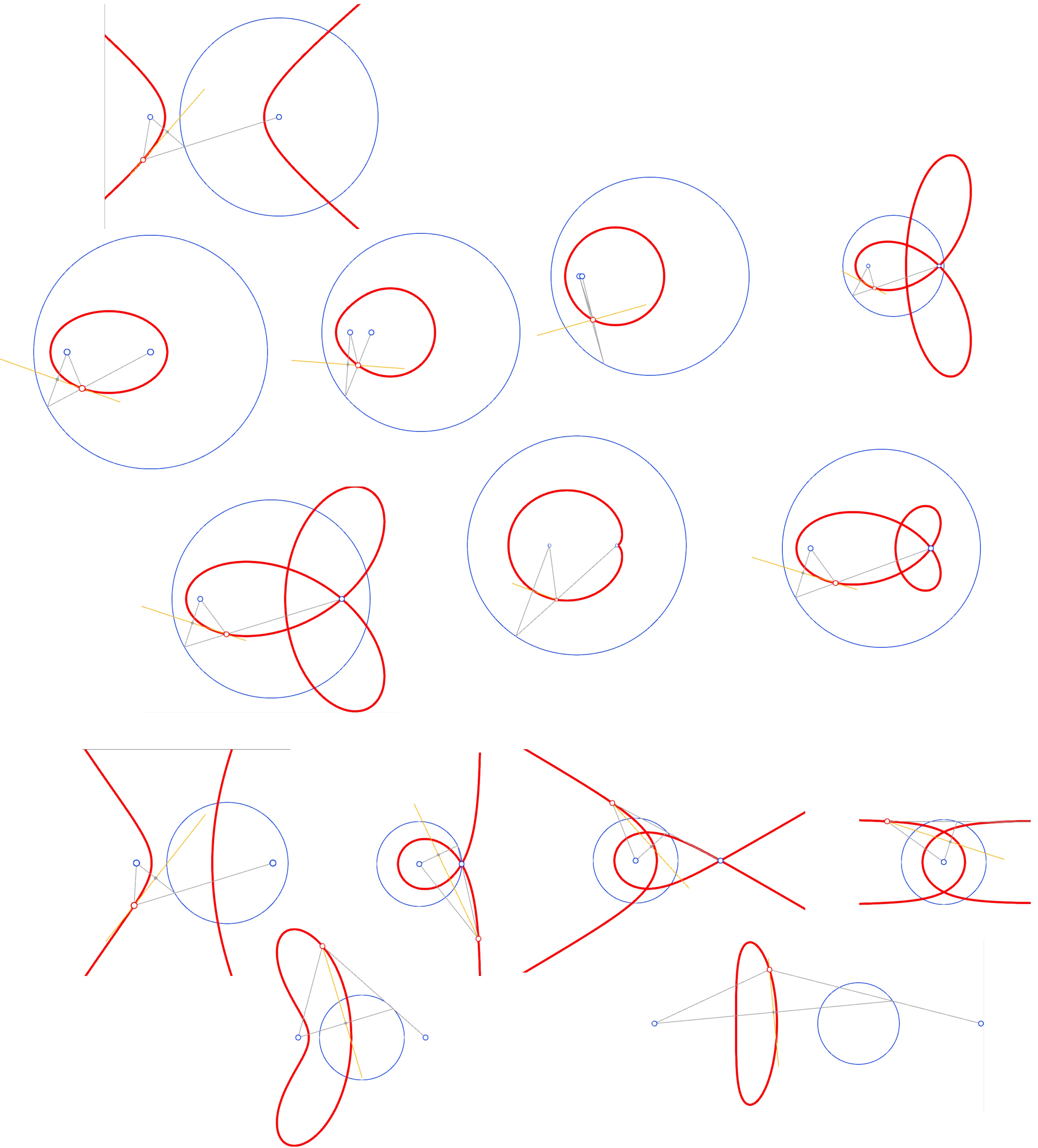
A short summary:
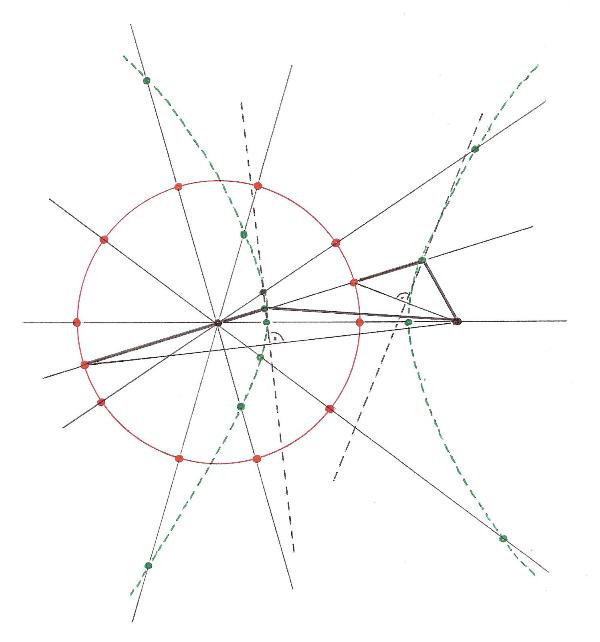
GENERAL CONSTRUCTION OF THE CURVES BY MEANS OF A CIRCLE AND TWO POINTS.
(Construction by perpendicular bisector.)
B and D can be anywhere in the plane of the circle.
There are three groups of the curves from this construction:
I) CONIC SECTIONS
D is in the center of the circle.
II) GENERALIZED CONIC SECTIONS (with symmetry axis)
B,D,M are on the same straight line.
D is outside the center of the circle.
III) GENERALIZED CONIC SECTIONS (without symmetry axis)
B,D,M are not on the same straight line. ("They form a triangle.")
Supplement:
Prof. Dr. Anton Gfrerrer made some remarks about these curves (in German) and made it available to incorporate on this page (download pdf).
And now the continuation of "CONIC SECTIONS AND THEIR SPECIAL CASES".
The half line:
|
|
|
The half line is a special case of the branch of the
hyperbola.
Two half lines are a special case of the hyperbola. (two fixed circles)
The point:
|
AB + AD = e + 0 = e
|
|
The point is a special case of the ellipse.
ANOTHER PROOF THAT THE CIRCLE AND THE PARABOLA ARE THE SPECIAL CASES OF THE ELLIPSE
A few equations from the common drawing:
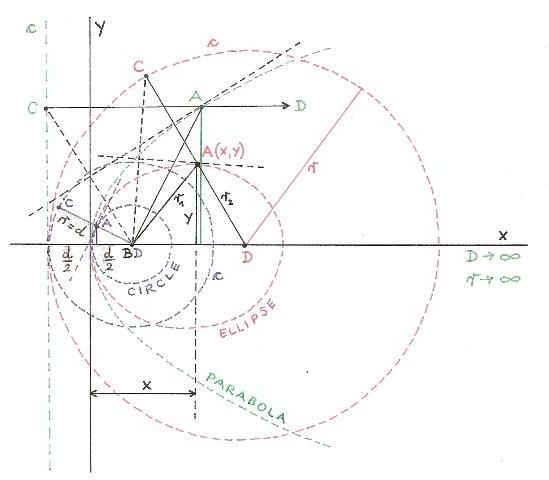
r is the radius of the fixed circle c; ( r instead of e)
d is the distance between B and c
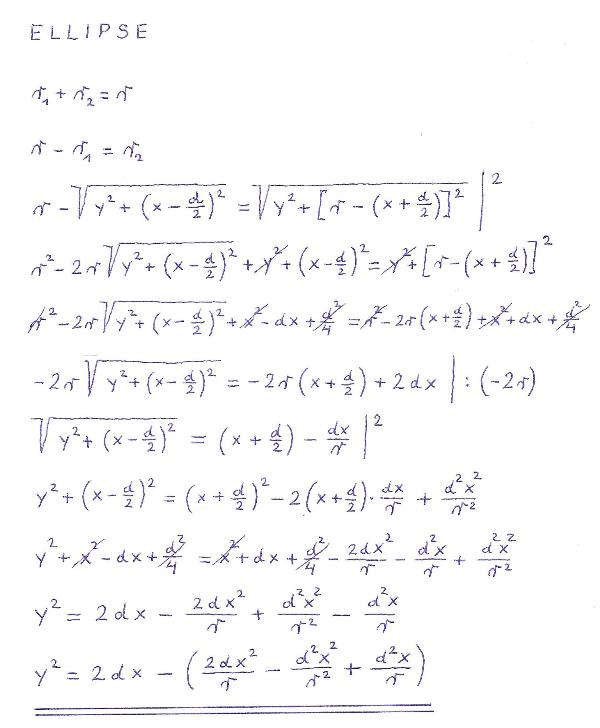
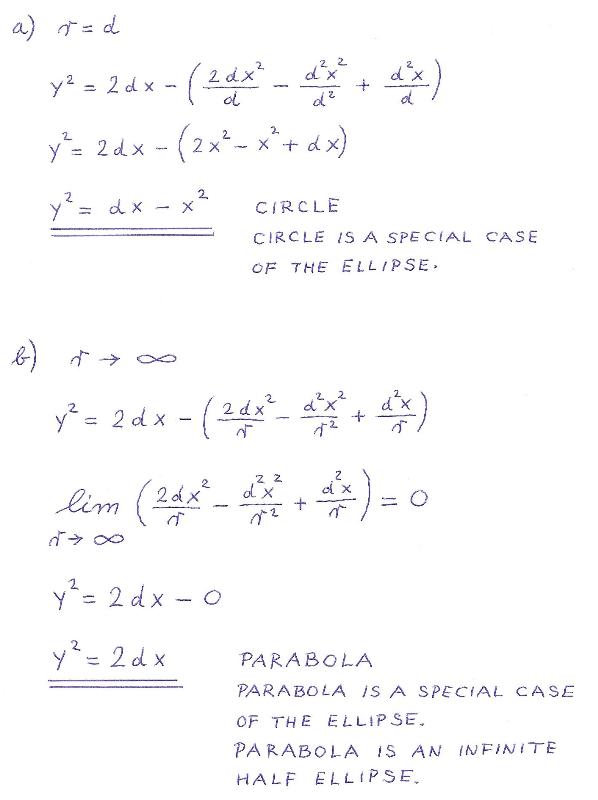
SUPPLEMENT 3 (25.05.2011):
HYPERBOLA
DEFINITION BY MEANS OF THE PAIRS OF POINTS ON THE STRAIGHT LINES THROUGH THE CENTRE OF THE FIXED CIRCLE
DEFINITION BY MEANS OF THE PAIRS OF POINTS ON THE STRAIGHT LINES THROUGH THE CENTRE OF THE FIXED CIRCLE
Another interpretation of the construction of the
hyperbola by means of one fixed point (focus) and one fixed circle.
THE BOTH BRANCHES OF THE HYPERBOLA ARE DEFINED.
WHAT IS NEW ABOUT THE CONIC SECTIONS ON THIS WEBSITE:
1) THE COMMON CONSTRUCTION AND DEFINITION OF ALL CONIC SECTIONS (ALSO OF THE PARABOLA) BY MEANS OF ONE FIXED CIRCLE AND ONE FIXED POINT.
2) THE WAY OF ILLUSTRATION OF AN ABSTRACT PARABOLA AT INFINITY.
3) THE DEFINITION OF THE HYPERBOLA (ALSO OF THE ELLIPSE AND THE CIRCLE) BY MEANS OF THE PAIRS OF POINTS ON THE STRAIGHT LINES THROUGH THE CENTRE OF THE FIXED CIRCLE. (THE BOTH BRANCHES OF THE HYPERBOLA ARE DEFINED)
4) SUPPLEMENT (February 15, 2015): DISTORTED CONIC SECTIONS
And finally, a few words about the past time of the universe, apart from redshift. (This is not a quite different subject. The conic sections and the universe have much in common: elliptical orbits of celestial bodies, etc.)
SEARCH FOR EXTRATERRESTRIAL INTELLIGENCE AS THE PROOF FOR THE BEGINNING OF THE UNIVERSE.
In a universe of infinite past time, with the perpetual formation and disappearance of stars and planets (eternal universe theory, static universe theory, steady state universe theory, etc.), a huge number of extraterrestrial intelligences would come into being. Many of them would now be in our part of the universe.
The first signals should be already received.
But, there are no signals.
This means that in our part of Milky Way there are not many extraterrestrial intelligences. And so the past time of the universe is not infinite.
THE UNIVERSE MUST HAVE HAD A BEGINNING.
WHITE DWARFS, NEUTRON STARS AND STELLAR BLACK HOLES AS THE PROOF FOR THE BEGINNING OF THE UNIVERSE.
In a universe of infinite past time, the universe would be full of them. Many of them would be between the stars in our part of Milky Way. But, there are not many of them. Therefore, the past time of the universe is limited.
THE UNIVERSE MUST HAVE HAD A BEGINNING.
THE CHANGING OF THE UNIVERSE AS THE PROOF FOR ITS BEGINNING.
The universe is changing. It is getting older and colder. (That's what we know today.) In a universe of infinite past time, this "getting older and colder" would have no beginning. "Getting older and colder" would take infinitely long. This means that the universe would be now infinitely old, with temperature at infinity near absolute zero.
But that is not true, because we exist in the universe that is not so old and cold.
THEREFORE, THE UNIVERSE MUST HAVE HAD A BEGINNING.
On an arbitrary straight line through the centre of
the fixed circle there is a pair of points, where every single point is
equidistant from
one fixed point (focus) and from one of two points of
intersection between the straight line and the fixed circle.
(Of course, that applies to the ellipse and the
circle, too.)
HYPERBOLA IS (ELLIPSE IS...; CIRCLE IS...) THE
GEOMETRIC LOCUS (THE SET) OF ALL PAIRS OF POINTS ON THE STRAIGHT
LINES THROUGH THE CENTRE OF THE FIXED CIRCLE, WHERE EVERY SINGLE POINT OF A PAIR OF POINTS ON AN ARBITRARY
STRAIGHT LINE IS EQUIDISTANT FROM ONE FIXED POINT (FOCUS) AND FROM ONE OF TWO POINTS OF INTERSECTION
BETWEEN THE STRAIGHT LINE AND THE FIXED CIRCLE.
LINES THROUGH THE CENTRE OF THE FIXED CIRCLE, WHERE EVERY SINGLE POINT OF A PAIR OF POINTS ON AN ARBITRARY
STRAIGHT LINE IS EQUIDISTANT FROM ONE FIXED POINT (FOCUS) AND FROM ONE OF TWO POINTS OF INTERSECTION
BETWEEN THE STRAIGHT LINE AND THE FIXED CIRCLE.
NOTE:
A similar definition (also the drawing) by means of
the pairs of points is applicable to the hyperbola (the
ellipse and the circle, too) on my
website www.zvone.com/math/curves/curves.html (drawings:
2a, 1a, 1c), relating the auxiliary circle k3 and the centre M2 of the
fixed
circle k2.
The both branches of the hyperbola are
defined.
WHAT IS NEW ABOUT THE CONIC SECTIONS ON THIS WEBSITE:
1) THE COMMON CONSTRUCTION AND DEFINITION OF ALL CONIC SECTIONS (ALSO OF THE PARABOLA) BY MEANS OF ONE FIXED CIRCLE AND ONE FIXED POINT.
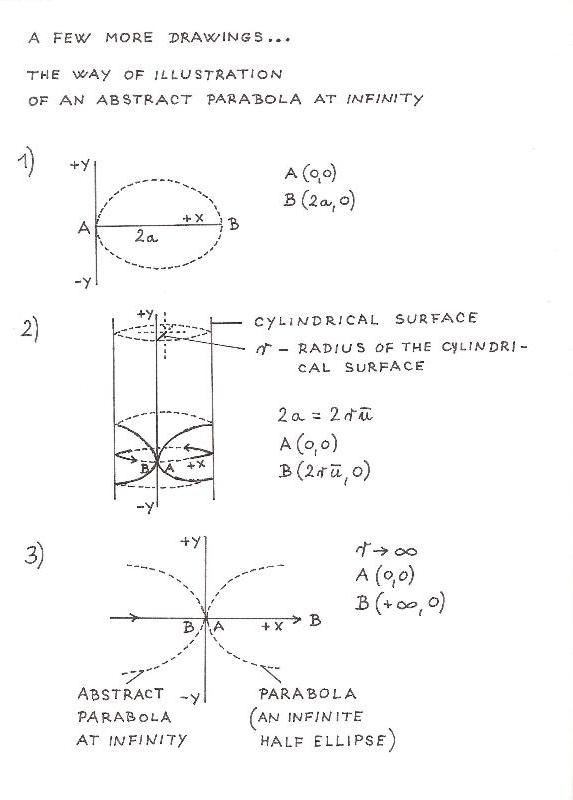
2) THE WAY OF ILLUSTRATION OF AN ABSTRACT PARABOLA AT INFINITY.
3) THE DEFINITION OF THE HYPERBOLA (ALSO OF THE ELLIPSE AND THE CIRCLE) BY MEANS OF THE PAIRS OF POINTS ON THE STRAIGHT LINES THROUGH THE CENTRE OF THE FIXED CIRCLE. (THE BOTH BRANCHES OF THE HYPERBOLA ARE DEFINED)
4) SUPPLEMENT (February 15, 2015): DISTORTED CONIC SECTIONS
And finally, a few words about the past time of the universe, apart from redshift. (This is not a quite different subject. The conic sections and the universe have much in common: elliptical orbits of celestial bodies, etc.)
SEARCH FOR EXTRATERRESTRIAL INTELLIGENCE AS THE PROOF FOR THE BEGINNING OF THE UNIVERSE.
In a universe of infinite past time, with the perpetual formation and disappearance of stars and planets (eternal universe theory, static universe theory, steady state universe theory, etc.), a huge number of extraterrestrial intelligences would come into being. Many of them would now be in our part of the universe.
The first signals should be already received.
But, there are no signals.
This means that in our part of Milky Way there are not many extraterrestrial intelligences. And so the past time of the universe is not infinite.
THE UNIVERSE MUST HAVE HAD A BEGINNING.
WHITE DWARFS, NEUTRON STARS AND STELLAR BLACK HOLES AS THE PROOF FOR THE BEGINNING OF THE UNIVERSE.
In a universe of infinite past time, the universe would be full of them. Many of them would be between the stars in our part of Milky Way. But, there are not many of them. Therefore, the past time of the universe is limited.
THE UNIVERSE MUST HAVE HAD A BEGINNING.
THE CHANGING OF THE UNIVERSE AS THE PROOF FOR ITS BEGINNING.
The universe is changing. It is getting older and colder. (That's what we know today.) In a universe of infinite past time, this "getting older and colder" would have no beginning. "Getting older and colder" would take infinitely long. This means that the universe would be now infinitely old, with temperature at infinity near absolute zero.
But that is not true, because we exist in the universe that is not so old and cold.
THEREFORE, THE UNIVERSE MUST HAVE HAD A BEGINNING.
Start Page