|
Author: |
Zvonimir Durcevic |
|
Address: |
Kaiser-Ebersdorfer Straße 28-38/12/3, 1110 Vienna, Austria |
|
EMail: |
|
|
Date: |
09.10.2005 |
Im April 2005 machte ich die Arbeit:
KREISSEHNEN-KURVEN (Kreis-Konchoiden)
Die Gerade, die Hundekurve, usw. aus der Kreissehnenkonstruktion
Mit den Bezeichnungen in alphabetischer Reihenfolge
|
a |
- Achse |
|
b |
- Kreis |
|
B |
- Punkt von b |
|
c |
- Radius von b |
|
C |
- Mittelpunkt von b |
|
d |
- Kreissehne |
|
D |
- Schnittpunkt der Kreissehnen |
|
d1 |
- größte Kreissehne (d1 = 2c) |
|
d2 |
- kleinste Kreissehne (d2 is senkrecht auf d1) |
|
e |
- Kreissehnen-Kurve |
|
E |
- Punkt von e |
|
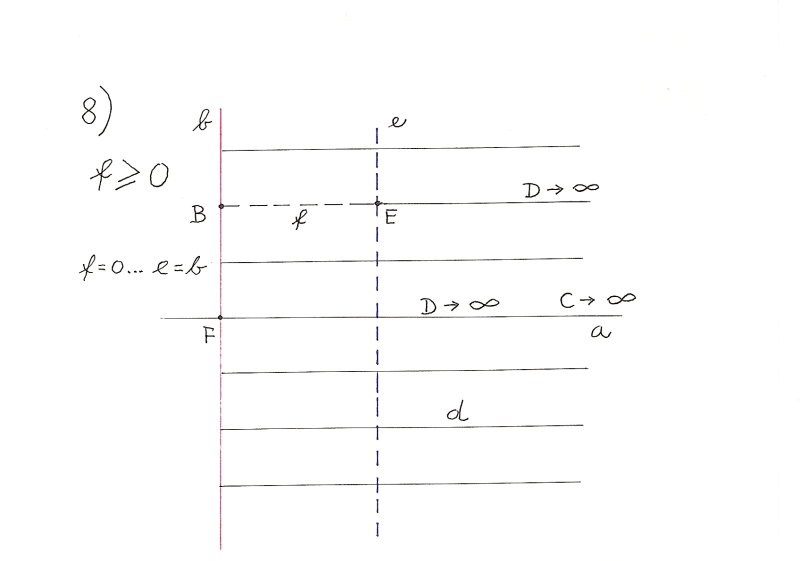
f |
- Abschnitt der Kreissehne (f = BE) |
|
F, G |
- Schnittpunkte von a und b (D ist der Punkt von CF) |
|
G |
- kleinster Abstand zwischen b und D (g = DF) |
|
h |
- gröster Abstand zwischen b und D (h = DG); g + h = d1 = 2c |
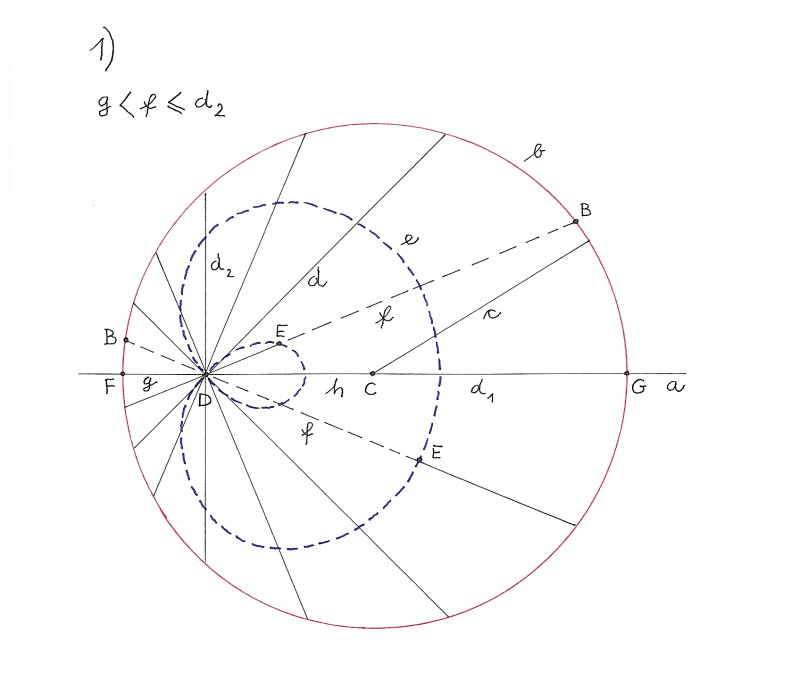
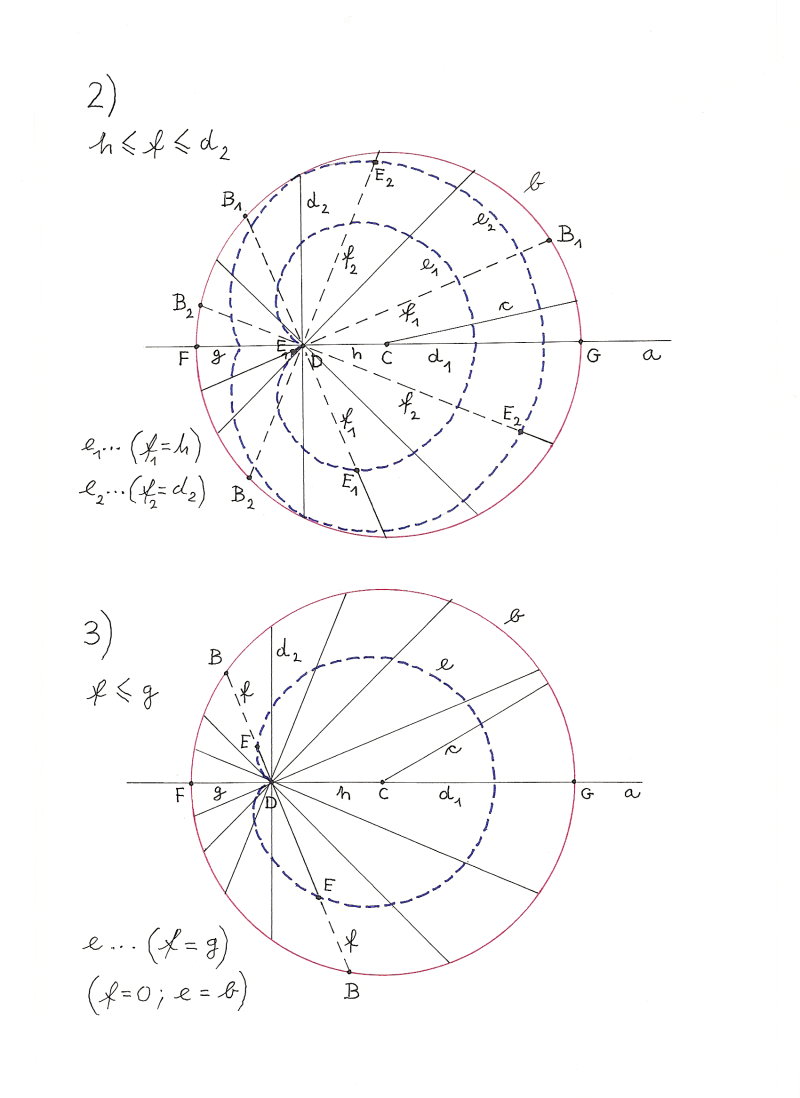
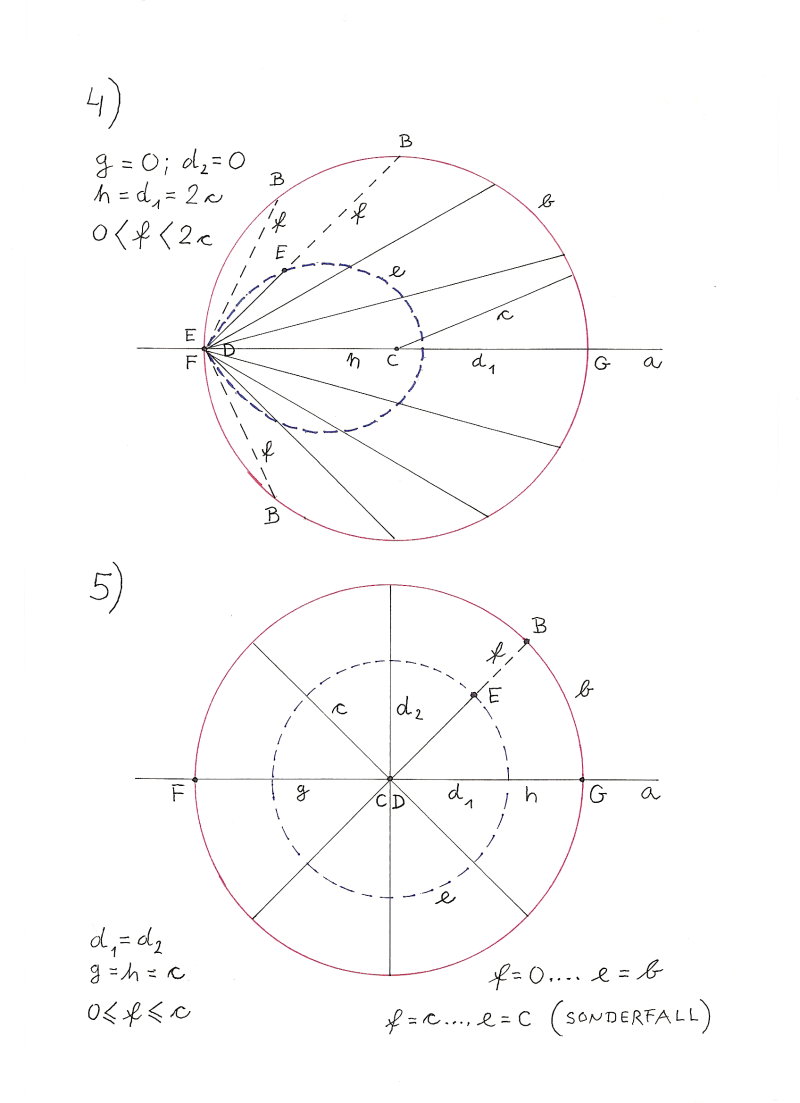
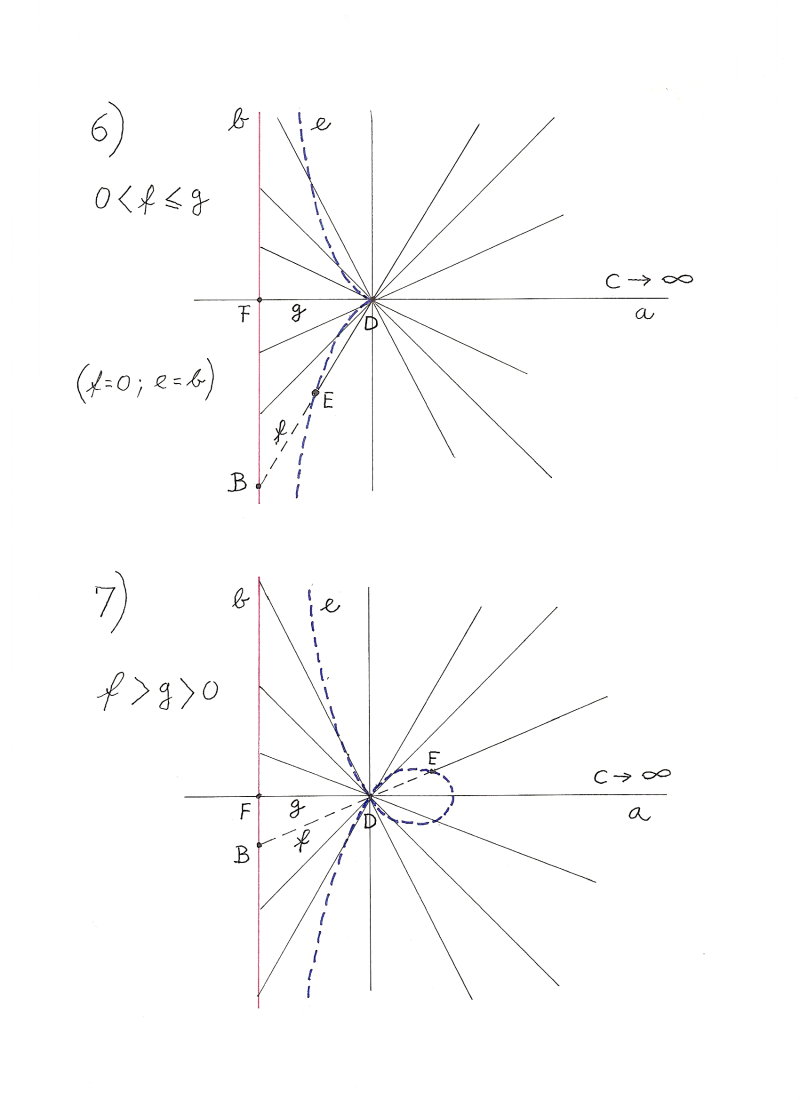
Für jede Kreissehnen-Kurve gilt:
Alle f haben dieselbe Länge.
f <= d2
Kein Punkt der Kreissehnen-Kurve liegt außerhalb des Kreises.
Parameter c, f, g, h bestimmen die Form und Größe der Kreissehnen-Kurve.





Die Gerade ist ein Sonderfall der Kreissehnen-Kurve.
Die Sehnenkonstruktion der Kurven gilt nicht nur innerhalb des Kreises, sondern auch innerhalb der anderen Kurven (z.B. innerhalb der Ellipse, usw.).
Innerhalb der Ellipse entstehen die Kurven aus der Ellipsensehnenkonstruktion.
ELLIPSENSEHNEN-KURVEN
Kein Punkt der Ellipsensehnen-Kurve liegt außerhalb der
Ellipse.
Die Form der Ellipse, die Position des Schnittpunktes der
Ellipsensehnen und der Abschnitt der Ellipsensehnen bestimmen die
Form der Ellipsensehnen-Kurve.
Position des Schnittpunktes der Ellipsensehnen innerhalb der
Ellipse:
a) Er liegt auf der Hauptachse:
Ellipsensehnen-Kurven
sind symetrisch zur Hauptachse.
b) Er liegt auf der
Nebenachse:
Ellipsensehnen-Kurven sind symetrisch zur
Nebenachse.
c) Er liegt im Mittelpunkt:
Ellipsensehnen-Kurven
sind symetrisch zu den beiden Achsen.
d) Er liegt nicht auf den
Achsen:
Ellipsensehnen-Kurven sind unsymetrisch.
Es gibt viele Formen der Ellipsensehnen-Kurven.
Mit Hilfe
dieses Textes ist es leicht sie zu zeichnen (konstruieren).
Selbstverständlich, diese Kreissehnen (Ellipsensehnen) sind
die Teile der Kreissekanten (Ellipsensekanten), die sich in einem
Punkt schneiden.
Deshalb sind die Kreissehnenkurven (Ellipsensehnenkurven) ein
Sonderfall der KREISSEKANTENKURVEN (ELLIPSENSEKANTENKURVEN).
Sie liegen innerhalb des Kreises (der Ellipse).
Es gibt viele Kreissekantenkurven (Ellipsensekantenkurven), die den Kreis (die Ellipse) schneiden, und viele, die außerhalb des Kreises (der Ellipse) liegen.
Durch Rotation dieser Kurven um die Achsen entstehen die
dreidimensionalen Flächen (bzw. Körper):
KUGELSEHNENFLÄCHEN; KUGELSEHNENKÖRPER; USW.
Empfehlenswerte Internetseite (Kreis-Konchoiden) von Prof.Dr. Dörte Haftendorn (Uni-Lüneburg Deutschland):
http://haftendorn.uni-lueneburg.de/mathe-lehramt/kurven/hoehere/konchoiden/kreis-konchoiden.htm
The construction of the curves by means of the chords of the
circle.
The shape of these curves is determined by c, f, g, h.
Of course, there is also the construction of the curves by means of the chords of the ellipse, etc.
Last Updated: 02.02.2010